Partager la publication "Angèle – Est-ce vraiment le Brol ?"
Pour cette fin d’année, intéressons-nous à un sujet plus léger, à savoir la chanteuse Angèle et son album Brol.
Véritable phénomène de l’année 2018, la chanteuse belge Angèle, jusque là inconnue du grand public, a réussi a être couronnée d’un disque de platine pour son premier album « Brol » le 6 décembre 2018, soit seulement 2 mois après sa sortie.

La question qui vous brûle les lèvres est je le sens : « Mais… cet album, est-ce vraiment le brol ?
C’est ce que nous allons analyser.
Avant profitons-en pour Tout Oublier :
Dans cette étude nous allons nous intéresser à la distribution des vers des chansons d’Angèle en fonction de la taille en caractères.
De quoi aurons nous besoin ?
Logiciel R
Comme précédemment, merci de télécharger Le Logiciel R sur ce site https://cran.r-project.org/, ainsi que l’environnement de développement RStudio ici : https://www.rstudio.com/products/rstudio/download/, afin de pouvoir tester vous même le code source.
Fichier de données
Nous avons créé un fichier Excel qui regroupe l’ensemble des vers des chansons de l’album Brol. installez le dans le même répertoire que votre projet R.
Code Source
Vous pouvez copier/coller les morceaux de code source dans un script R pour les tester.
Vous pouvez aussi téléchargez gratuitement le code source en entier dans notre boutique à l’adresse : https://www.anakeyn.com/boutique/produit/script-r-angele-debrolisee/
Chargement des bibliothèques
Attention ! si vous n’avez pas installé certains packages dans votre environnement RStudio, vous devez dé-commenter ceux qui vous intéressent.
#
####################################################
#Angèle - Est-ce vraiment le brol ?
####################################################
# Installation de l'environnement
####################################################
#Intallation des packages (une fois)
#install.packages("ggplot2")
#install.packages("readxl")
#install.packages("tm") #une fois
#install.packages("qdap") #une fois
#install.packages("wordcloud")
#install.packages("RWeka")
#install.packages("stringi")
#install.packages("BSDA")
#install.packages("dplyr")
#Chargement des bibliothèques
library(ggplot2)
library(readxl) #pour read_excel ...
library(tm) #pour le text mining : Vectorsource(), VCorpus() et le nettoyage removeSparseTerms
library(qdap) #Aussi pour text mining et nettoyage de texte
library(wordcloud) #Nuages de mots clés.
library(RWeka) #pour Weka_control (utilisé pour la création de bigrammes, trigrammes )
library(stringi) #pour stri_replace_all_fixed(x, " ", "")
library(BSDA) #pour SIGN.test
library(dplyr) #pour slice
#######################################################################################
#Recupération du texte des chansons de Brol d'Angèle
#nous avons tout mis dans un fichier .xlsx chaque ligne représente un vers !!!!
angeleBrol <- read_excel("Angele-Brol.xlsx")
angeleBrol$lineLength <- nchar(angeleBrol$line) #calcul de la longueur des vers.
str(angeleBrol) #regardons ce que nous avons
Le fichier récupéré a la structure suivante :
Classes ‘tbl_df’, ‘tbl’ and 'data.frame': 519 obs. of 7 variables: $ numTitle : num 1 1 1 1 1 1 1 1 1 1 ... $ title : chr "La Thune" "La Thune" "La Thune" "La Thune" ... $ numElement: num 1 1 1 1 1 1 1 1 2 2 ... $ element : chr "couplet" "couplet" "couplet" "couplet" ... $ numLine : num 1 2 3 4 5 6 7 8 9 10 ... $ line : chr "Tout le monde il veut seulement la thune" "Et seulement ça, ça les fait bander" "Tout le monde il veut seulement la fame" "Et seulement ça, ça les fait bouger" ... $ lineLength: int 40 35 39 35 36 30 31 35 19 38 ...
J’ai aussi divisé chaque morceau en parties : « couplet », « refrain », « intro », « pont », « outro » mais nous ne nous en servirons pas ici.
Normalité de l’album
En premier lieu vérifions la normalité de l’album !! Ici, nous utilisons un test de shapiro. Si la p valeur < 0.05 la normalité n’est pas retenue.
##################################################################
#Verification normalité de la distribition des vers de tout l'album
myPValue <- shapiro.test(angeleBrol$lineLength)$p.value #verification de la normalité
#p-value = 1.521e-11 <<< 0.05 la loi n'est pas normale : c'est le brol !!!
#§Grahique
#calcul de la bonne bindwidth #si on préfere un histogram
x <- angeleBrol$lineLength
hist(x,breaks="FD")
breaks <- pretty(range(x), n = nclass.FD(x), min.n = 1)
bwidth <- breaks[2]-breaks[1]
##############################################################
ggplot(data=angeleBrol, aes(x=lineLength)) +
# geom_histogram(binwidth=bwidth ) +
geom_density(color="blue") +
xlab("Nombre de vers") +
ylab("Densité") +
labs(title = "La loi n'est pas normale.",
subtitle = paste("la pvaleur = ", format(myPValue, scientific=FALSE) , " << 0.05. C'est le brol."),
caption = "Courbe de distribution du nombre de vers selon la taille")
##################################################################
#sauvegarde du dernier ggplot
ggsave(filename = "AngeleBrolDistribution.jpeg", dpi="print")
Visualisons le graphique :
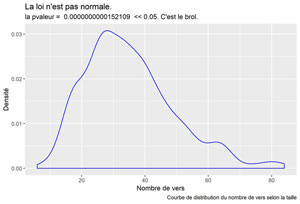
Normalité des chansons
Testons la normalité chanson par chanson :
##################################################################
# Normalité par chanson
lineNChar <- vector()
myShapiroTest <- data.frame(p.value = double())
for (i in 1:12) {
lineNChar <- angeleBrol[which(angeleBrol$numTitle==i), "lineLength"]
myShapiroTest[i,"p.value" ] <- shapiro.test(lineNChar$lineLength)$p.value
}
str(myShapiroTest$p.value)
ggplot(data=myShapiroTest, aes(x=as.numeric(rownames(myShapiroTest)), y=p.value)) +
geom_line() +
geom_hline(yintercept = 0.05, color = "red") +
scale_x_discrete(name="Numéro de Chanson", limits=c(1,2,3,4,5,6,7,8,9,10,11,12)) +
ylab("P Valeur") +
labs(title = "Aucune distribution n'est normale.",
subtitle = "Toutes les p.valeurs sont < 0.05. C'est le brol.",
caption = "P valeur du test de shapiro pour chacune des chansons.")
ggsave(filename = "AngeleBrolNormalTest.jpeg", dpi="print") #sauvegarde du dernier ggplot
Visualisons le graphique :
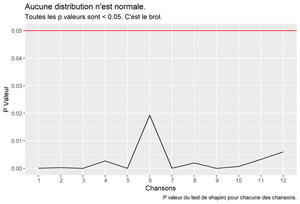
Distributions par chanson
Regardons les courbes de densité chanson par chanson :
##################################################################
#Distributions par chanson
for (i in 1:12) {
songTitle <- unique(angeleBrol[which(angeleBrol$numTitle ==i), "title"])
pValeur <- myShapiroTest[i,"p.value" ]
ggplot(data=angeleBrol[which(angeleBrol$numTitle ==i),], aes(x=lineLength)) +
geom_density(color="blue") +
xlab("Nombre de vers") +
ylab("Densité") +
labs(title = "La distribution n'est pas normale.",
subtitle = paste("la p Valeur est ", format(pValeur, scientific=FALSE), " < 0.05. C'est le brol."),
caption = paste("Courbe de distribution du nombre de vers selon la taille pour ", songTitle ))
ggsave(filename = stri_replace_all_fixed(paste("AngeleBrolSong-",i,".jpeg"), " ", ""), dpi="print") #sauvegarde du dernier ggplot
}
La Thune
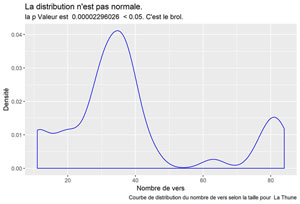
Balance ton quoi
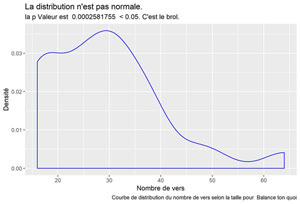
Jalousie
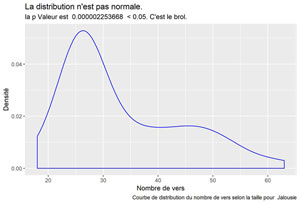
Tout oublier
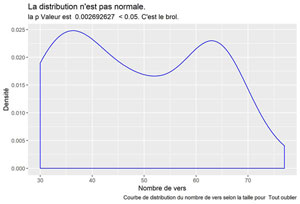
La Loi de Murphy
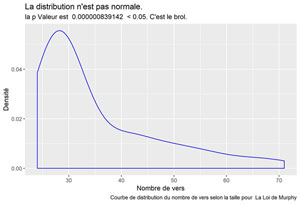
Nombreux
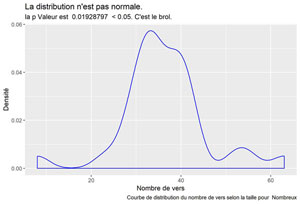
rem : c’est celle qui ressemble le plus à une courbe normale
Victime des réseaux
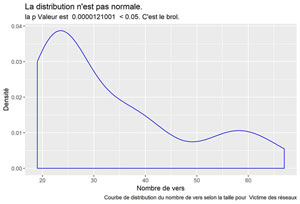
Les Matins
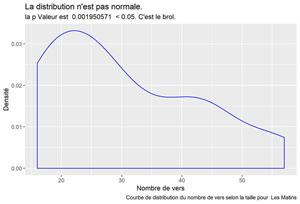
Je veux tes yeux
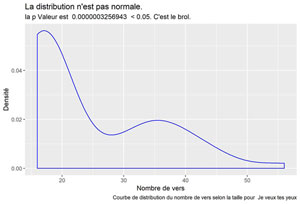
Ta Reine
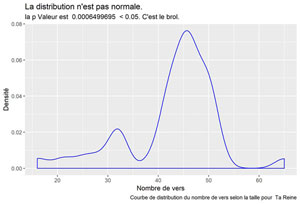
Flemme
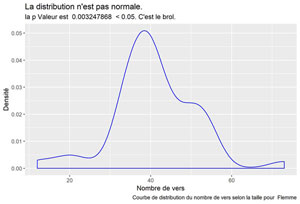
Flou
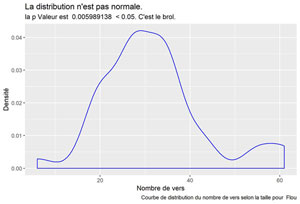
Comparatif des distributions
Essayons de comparer les distributions sur un seul graphique :
#Comparons les chansons !! pas très lisible.
ggplot(data=angeleBrol, aes(x=lineLength, color=title)) +
geom_density()
xlab("Nombre de vers") +
ylab("Densité") +
labs(title = "Aucune loi n'est normale.",
subtitle = "C'est le brol. en plus c'est illisible !",
caption = "Courbe de distribution du nombre de vers selon la taille par chanson")
ggsave(filename = "AngeleBrolAllSongsDist.jpeg", dpi="print") #sauvegarde du dernier ggplot en fonction du mois
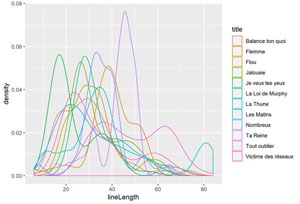
Le graphique n’est pas très lisible : c’est le brol !
Comparatif des chansons deux à deux
pour cela nous allons utiliser le SIGN.test de R.
i.e
hypothèses :
- Hypothèse nulle : La médiane des différences entre les paires de longueurs de vers des 2 chansons est égal à zéro
- Hypothèse alternative : La médiane des différences entre les paires de longueurs de vers des 2 chansons est différente de zéro.
si la p.valeur > 0.05 l’hypothèse nulle n’est pas rejetée.
############################################################"
# Comparatif des chansons deux à deux avec SIGN.Test
k=1
myMd <- 0 #médiane attendue différence entre la distribution x et la distribution y
myCl <- 0.95
biSongs <- data.frame(pValue=double(),
numSong1 = integer(),
numSong2 = integer(),
conf.int.inf = double(),
conf.int.sup = double(),
statistic = double(),
estimate = double())
for (i in 1:11) {
for (j in (i+1):12) {
lineNChar1 <- angeleBrol[which(angeleBrol$numTitle==i), "lineLength"]
lineNChar2 <- angeleBrol[which(angeleBrol$numTitle==j), "lineLength"]
NbLineMax <- min(nrow(lineNChar1),nrow(lineNChar2)) #x et y doivent être égaux on prend le plus petit possible
lineNChar1<- slice(lineNChar1, 1:NbLineMax)
lineNChar2<- slice(lineNChar2, 1:NbLineMax )
res <- SIGN.test(x=lineNChar1$lineLength, y=lineNChar2$lineLength , md=myMd, alternative="two.sided", conf.level = myCl)
#str(res)
biSongs[k, "pValue"] <- res$p.value
biSongs[k, "numSong1"] <- i
biSongs[k, "numSong2"] <- j
biSongs[k, "conf.int.inf"] <- res$conf.int[1] #borne inférieure de l'intervalle de confiance
biSongs[k, "conf.int.sup"] <- res$conf.int[2] #borne supérieure de l'intervalle de confiance
biSongs[k, "statistic"] <- res$statistic
biSongs[k, "estimate"] <- res$estimate
#Dessinons les comparatifs
songTitle1 <- unique(angeleBrol[which(angeleBrol$numTitle == i), "title"])
songTitle2 <- unique(angeleBrol[which(angeleBrol$numTitle == j), "title"])
ggplot() +
geom_density(data=lineNChar1, aes(x=lineLength), color="blue") +
geom_density(data=lineNChar2, aes(x=lineLength), color="red") +
xlab("Nombre de vers") +
ylab("Densité") +
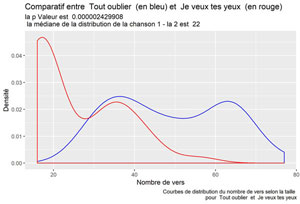
labs(title = paste("Comparatif entre ", songTitle1, " (en bleu) et ", songTitle2," (en rouge)"),
subtitle = paste("la p Valeur est ", format(res$p.value, scientific=FALSE), "\n la médiane de la distribution de la chanson 1 - la 2 est ", res$estimate),
caption = paste("Courbes de distribution du nombre de vers selon la taille \n pour ", songTitle1, " et ", songTitle2 ))
ggsave(filename = stri_replace_all_fixed(paste("AngeleBrolSongs-",i,"-",j,"-", k, ".jpeg"), " ", ""), dpi="print") #sauvegarde du dernier ggplot
#############
k <- k+1 # suivant
}
}
#Pour trouver le plus 'ressemblant ' et le plus "différent "
#avec la pValue
which.max(biSongs$pValue)
which.min(biSongs$pValue)
#avec Estimate : median of x-y
which.min(abs(biSongs$estimate))
which.max(abs(biSongs$estimate))
nbBisongs <- nrow(biSongs)
nbEquBisongs <- nrow(biSongs[which(biSongs$pValue > 0.05),])
ggplot(data=biSongs, aes(x="", y=pValue)) +
geom_violin() +
geom_hline(yintercept = 0.05, color="red") +
xlab("") +
ylab("P-Valeur") +
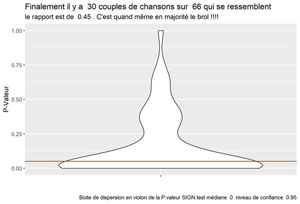
labs(title = paste("Finalement il y a ", nbEquBisongs, "couples de chansons sur ", nbBisongs, "qui se ressemblent" ),
subtitle = paste("le rapport est de ", round(nbEquBisongs / nbBisongs, digits=2), ". C'est quand même en majorité le brol !!!!"),
caption = paste("Boite de dispersion en violon de la P.valeur SIGN.test médiane ", myMd, " niveau de confiance ", myCl))
#sauvegarde du dernier ggplot
ggsave(filename = "biSongsPvalue.jpeg", dpi="print")
Les chansons les plus « ressemblantes » sont :
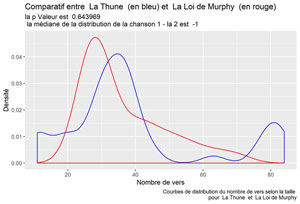
Les chansons les plus « différentes » sont :
Visualisons la boite de dispersion pour l’ensemble des p valeurs :
Conclusion
Bon ben c’est bien le brol !
Je vous souhaite de bonnes fêtes !