Partager la publication "Modèle Interne : test de classification de pages via le Machine Learning pour un seul site"
Cet article fait suite aux 2 articles précédents :
- Classification de pages Web pour le SEO via le Machine Learning avec Python
- Récupérez des données de positionnement de vos pages via Google Search Console API
Dans cet article nous allons tester un modèle « interne » de classification de pages au moyen du machine learning pour un seul site.
Dans notre cas nous partons des données de Pages/Expressions/Positions récupérées via Google Search console API pour le site de Networking Morbihan pour le mois de Mai 2019. Le jeu de données contient 514 enregistrements et les variables suivantes :
- clicks ; clics obtenus par le couple page/expression
- ctr : click through rate : taux de clics clics/impressions
- impressions : nombre d’affichage de la page de mon site dans les pages des résultats de recherche (SERPs Search Engine Results Pages) dans Google.
- Position : position de ma page dans les SERPs
- query : requête, on dit aussi indifféremment « expression » ou « mot clé » ou « groupe de mots clés »…
- page : l’url de la page
Pour ce premier test nous allons construire des variables explicatives à partir des données que nous avons :
- isHttps : le site est -il en https ?*
- level : « pseudo niveau » de la page dans l’arborescence du site
- lenWebsite : taille de l’url du site en caractères
- lenTokensWebSite : taille de l’url du site en nombre de mots
- lenTokensQueryInWebSiteFrequency : fréquence des mots de la requête dans le nom du site.
- sumTFIDFWebSiteFrequency : somme des TF*IDF** pour les mots de WebSite en fonction de la taille en mots (indicateur d’originalité du contenu).
- lenPath : taille du chemin*** en caractères
- lenTokensPath : taille du chemin en nombre de mots
- lenTokensQueryInPathFrequency : fréquence des mots de la requête dans le chemin.
- sumTFIDFPathFrequency : idem que pour WebSite.
*ici nous sommes sur un seul site et toutes nos pages sont en https, ce qui n’a pas beaucoup d’intérêt. On garde cette information pour la suite.
**TF*IDF (Term Frequency * Inverse Document Frequency), nous reviendrons la dessus plus bas.
***Le chemin
correspond ici à la partie de l’URL après le site Web par exemple dans :
https://www.networking-morbihan.com/comment-financer-son-entreprise-le-9-avril-2019-a-larmor-plage
webSite : https://www.networking-morbihan.com
et le chemin « path » : « comment-financer-son-entreprise-le-9-avril-2019-a-larmor-plage »
TF*IDF : Term Frequency * Inverse Document Frequency
Pendant de nombreuses années, en SEO, il suffisait de mettre de nombreux mots clés sur votre page en fonction de la thématique pour pouvoir avoir des chances de ressortir dans les résultats des moteurs de recherche.
Aujourd’hui c’est un peu plus complexe, et il vous est demandé de faire preuve d’originalité en créant des contenus uniques mais pertinents pour vous distinguer de vos concurrents.
Une méthode pour contrôler l’originalité des termes de votre document par rapport à un univers de concurrence, est de calculer le TF*IDF pour chacun de ceux-ci.
Le principe du TF*IDF est de calculer le poids d’un terme dans un document relativement à un ensemble de documents (souvent appelé corpus).
La formule est la suivante : pour le « poids » (weight en anglais) d’un terme i dans un document j :
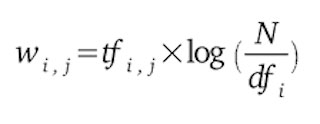
Où :
| : nombre d’occurrences de i dans j. | |
| : nombre de documents contenant i | |
| N | : nombre total de documents |
Ici comme nous ne souhaitons pas mesurer l’originalité de chacun des termes dans une variable, mais l’originalité globale de la variable nous sommons les TF*IDF et les divisons par la taille de la variable en nombre de termes.
Pour ceux qui suivent 🙂 : Ici on regarde cet indicateur notamment pour la variable WebSite : ceci n’a pas beaucoup d’intérêt puisque c’est la même pour tout le monde.
Cet indicateur n’aura de sens ici que pour la variable « path » : sumTFIDFPathFrequency
Rappel : pour simplifier le problème nous classifions ici en 2 groupes : les pages dans le Top10 et les autres.
De quoi aurons nous besoin ?
Python Anaconda
Anaconda est une version de Python dédiée aux Data Sciences. Rendez vous sur la page de téléchargement d’Anaconda Distribution pour télécharger la version qui vous convient selon votre ordinateur. Remarque : nous faisons tourner le programme dans l’IDE Spyder fourni avec Anaconda.
Jeu de données
Nous partons du jeu de données créé lors de la phase précédente. Vous pouvez télécharger l’archive contenant ces données sur notre GitHub. Dézipper le fichier dans le répertoire qui contient votre programme source Python.
Code Source
vous pouvez copier/coller les morceaux de code source suivant ou télécharger l’ensemble du code gratuitement à partir de notre boutique : https://www.anakeyn.com/boutique/produit/script-python-machine-learning-un-site/
Récupération des bibliothèques utiles et du jeu de données
# -*- coding: utf-8 -*-
"""
Created on Wed Jun 19 18:39:18 2019
@author: Pierre
"""
##########################################################################
# GSCOneSiteMachineLearning - modifié le 26/11/2019
# Auteur : Pierre Rouarch - Licence GPL 3
# Test modele machine learning pour un site (données Google Search Console API)
# focus sur la précision du set de test plutot que le F1 Score global
###################################################################
# On démarre ici
###################################################################
#Chargement des bibliothèques générales utiles
import numpy as np #pour les vecteurs et tableaux notamment
import matplotlib.pyplot as plt #pour les graphiques
#import scipy as sp #pour l'analyse statistique
import pandas as pd #pour les Dataframes ou tableaux de données
import seaborn as sns #graphiques étendues
#import math #notamment pour sqrt()
import os
from urllib.parse import urlparse #pour parser les urls
import nltk # Pour le text mining
# Machine Learning
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
#Matrice de confusion
from sklearn.metrics import confusion_matrix
#pour les scores
from sklearn.metrics import f1_score #abandonné
#from sklearn.metrics import matthews_corrcoef
from sklearn.metrics import accuracy_score
import gc #pour vider la memoire
print(os.getcwd()) #verif
#mon répertoire sur ma machine - nécessaire quand on fait tourner le programme
#par morceaux dans Spyder.
#myPath = "C:/Users/Pierre/MyPath"
#os.chdir(myPath) #modification du path
#print(os.getcwd()) #verif
#Relecture des données Pages/Expressions/Positions ############
dfGSC = pd.read_json("dfGSC-MAI.json")
dfGSC.query
dfGSC.info() # on a 514 enregistrements.
Fonctions de calcul de la somme TF*IDF
Afin d’illustrer le calcul TF*IDF nous avons créé 2 fonctions qui permettent de calculer les sommes des TF*IDF à partir d’une variable donnée par une colonne de DataFrame.
Une des fonctions propose un calcul « à la main ». L’autre utilise la fonction TfidfVectorizer de la bibliothèque Scikit-Learn qui est plus rapide.
############################################
# Calcul de la somme des tf*idf
#somme des TF*IDF pour chaque colonne de tokens calculé à la main (plus lent)
def getSumTFIDFfromDFColumnManual(myDFColumn) :
tf = myDFColumn.apply(lambda x: pd.Series(x).value_counts(normalize=True)).fillna(0)
idf = pd.Series([np.log10(float(myDFColumn[0])/len([x for x in myDFColumn.values if token in x])) for token in tf.columns])
##################################################
idf.index = tf.columns
tfidf = tf.copy()
for col in tfidf.columns:
tfidf[col] = tfidf[col]*idf[col]
return np.sum(tfidf, axis=1)
#somme des TF*IDF pour chaque colonne de tokens calculé avec TfidfVectorizer
def getSumTFIDFfromDFColumn(myDFColumn) :
from sklearn.feature_extraction.text import TfidfVectorizer
corpus = myDFColumn.apply(' '.join)
vectorizer = TfidfVectorizer(norm=None)
X = vectorizer.fit_transform(corpus)
return np.sum(X.toarray(), axis=1)
Créations de variables explicatives
On va enrichir les données que l’on a pour créer de nouvelles variables explicatives pour créer un modèle de Machine Learning.
#########################################################################
# Détermination de variables techniques et construites à partir des
# autres variables
#########################################################################
#Creation des Groupes (variable à expliquer) :
# finalement on prend une classification Binaire
dfGSC.loc[dfGSC['position'] <= 10.5, 'group'] = 1
dfGSC.loc[dfGSC['position'] > 10.5, 'group'] = 0
#création de nouvelles variables explicatives
#Creation de variables d'url à partir de page
dfGSC['webSite'] = dfGSC['page'].apply(lambda x: '{uri.scheme}://{uri.netloc}/'.format(uri=urlparse(x)))
dfGSC['uriScheme'] = dfGSC['page'].apply(lambda x: '{uri.scheme}'.format(uri=urlparse(x)))
dfGSC['uriNetLoc'] = dfGSC['page'].apply(lambda x: '{uri.netloc}'.format(uri=urlparse(x)))
dfGSC['uriPath'] = dfGSC['page'].apply(lambda x: '{uri.path}'.format(uri=urlparse(x)))
#Est-ce que le site est en https ? ici ne sert pas vraiment car on n'a qu'un seul site
#en https.
dfGSC.loc[dfGSC['uriScheme']== 'https', 'isHttps'] = 1
dfGSC.loc[dfGSC['uriScheme'] != 'https', 'isHttps'] = 0
dfGSC.info()
#"Pseudo niveau" dans l'arborescence calculé au nombre de / -2
dfGSC['level'] = dfGSC['page'].str[:-1].str.count('/')-2
#définition du tokeniser pour séparation des mots
tokenizer = nltk.RegexpTokenizer(r'\w+') #définition du tokeniser pour séparation des mots
#on va décompter les mots de la requête dans le nom du site et l'url complète
#on vire les accents
queryNoAccent= dfGSC['query'].str.normalize('NFKD').str.encode('ascii', errors='ignore').str.decode('utf-8')
#on tokenize la requete sans accents
dfGSC['tokensQueryNoAccent'] = queryNoAccent.apply(tokenizer.tokenize) #séparation des mots pour la reqête
#Page
dfGSC['lenPage']=dfGSC['page'].apply(len) #taille de l'url complète en charactères
dfGSC['tokensPage'] = dfGSC['page'].apply(tokenizer.tokenize) #séparation des mots pour l'url entier
dfGSC['lenTokensPage']=dfGSC['tokensPage'].apply(len) #longueur de l'url en mots
#mots de la requete dans Page
dfGSC['lenTokensQueryInPage'] = dfGSC.apply(lambda x : len(set(x['tokensQueryNoAccent']).intersection(x['tokensPage'])),axis=1)
#total des fréquences des mots dans Page
dfGSC['lenTokensQueryInPageFrequency'] = dfGSC.apply(lambda x : x['lenTokensQueryInPage']/x['lenTokensPage'],axis=1)
#SumTFIDF
dfGSC['sumTFIDFPage'] = getSumTFIDFfromDFColumn(dfGSC['tokensPage'])
dfGSC['sumTFIDFPageFrequency'] = dfGSC.apply(lambda x : x['sumTFIDFPage']/(x['lenTokensPage']+0.01),axis=1)
#WebSite
dfGSC['lenWebSite']=dfGSC['webSite'].apply(len) #taille de l'url complète en charactères
dfGSC['tokensWebSite'] = dfGSC['webSite'].apply(tokenizer.tokenize) #séparation des mots pour l'url entier
dfGSC['lenTokensWebSite']=dfGSC['tokensWebSite'].apply(len) #longueur de l'url en mots
#mots de la requete dans WebSite
dfGSC['lenTokensQueryInWebSite'] = dfGSC.apply(lambda x : len(set(x['tokensQueryNoAccent']).intersection(x['tokensWebSite'])),axis=1)
#total des fréquences des mots dans WebSite
dfGSC['lenTokensQueryInWebSiteFrequency'] = dfGSC.apply(lambda x : x['lenTokensQueryInWebSite']/x['lenTokensWebSite'],axis=1)
#SumTFIDF
dfGSC['sumTFIDFWebSite'] = getSumTFIDFfromDFColumn(dfGSC['tokensWebSite'])
dfGSC['sumTFIDFWebSiteFrequency'] = dfGSC.apply(lambda x : x['sumTFIDFWebSite']/(x['lenTokensWebSite']+0.01),axis=1)
#Path
dfGSC['lenPath']=dfGSC['uriPath'].apply(len) #taille de l'url complète en charactères
dfGSC['tokensPath'] = dfGSC['uriPath'].apply(tokenizer.tokenize) #séparation des mots pour l'url entier
dfGSC['lenTokensPath']=dfGSC['tokensPath'].apply(len) #longueur de l'url en mots
#mots de la requete dans Path
dfGSC['lenTokensQueryInPath'] = dfGSC.apply(lambda x : len(set(x['tokensQueryNoAccent']).intersection(x['tokensPath'])),axis=1)
#total des fréquences des mots dans Path
#!Risque de division par zero on fait une boucle avec un if
dfGSC['lenTokensQueryInPathFrequency']=0
for i in range(0, len(dfGSC)) :
if dfGSC.loc[i,'lenTokensPath'] > 0 :
dfGSC.loc[i,'lenTokensQueryInPathFrequency'] =dfGSC.loc[i,'lenTokensQueryInPath']/dfGSC.loc[i,'lenTokensPath']
#SumTFIDF
dfGSC['sumTFIDFPath'] = getSumTFIDFfromDFColumn(dfGSC['tokensPath'])
dfGSC['sumTFIDFPathFrequency'] = dfGSC.apply(lambda x : x['sumTFIDFPath']/(x['lenTokensPath']+0.01),axis=1)
#Sauvegarde pour la suite
dfGSC.to_json("dfGSC1-MAI.json")
#on libere de la mémoire
dir() #pour savoir ce qu'il y a
del dfGSC
gc.collect()
Préparation des données pour le Machine Learning
On va préparer les données : déterminer les variables explicatives et la variable à expliquer et splitter le jeu de données en des données d’entrainement et des données de test.
#############################################################################
# Premier test de Machine Learning sur Environnement Interne et variables
# uniquement créés à partir des urls et des mots clés.
#############################################################################
#Préparation des données
#on libere de la mémoire
del dfGSC
gc.collect()
#Relecture ############
dfGSC1 = pd.read_json("dfGSC1-MAI.json")
dfGSC1.query
dfGSC1.info() # 514 enregistrements.
#on choisit nos variables explicatives
X = dfGSC1[['isHttps', 'level',
'lenWebSite', 'lenTokensWebSite', 'lenTokensQueryInWebSiteFrequency' , 'sumTFIDFWebSiteFrequency',
'lenPath', 'lenTokensPath', 'lenTokensQueryInPathFrequency' , 'sumTFIDFPathFrequency']] #variables explicatives
y = dfGSC1['group'] #variable à expliquer
#on va scaler
scaler = StandardScaler()
scaler.fit(X)
X_Scaled = pd.DataFrame(scaler.transform(X.values), columns=X.columns, index=X.index)
X_Scaled.info()
#onchoisit random_state = 42 en hommage à La grande question sur la vie, l'univers et le reste
#dans "Le Guide du voyageur galactique" par Douglas Adams. Ceci afin d'avoir le même split
#tout au long de notre étude.
X_train, X_test, y_train, y_test = train_test_split(X_Scaled,y, random_state=42)
Méthode des K-NN : k plus proches voisins
L’algorithme k-NN (k-plus proches voisins, en anglais k-nearest
neighbors) est un algorithme de machine learning assez simple. Ici, la construction du modèle consiste simplement à stocker l’ensemble d’apprentissage. Contrairement à d’autres algorithmes qui détermine un modèle mathématique.
Afin de faire une prévision sur une nouvelle donnée, l’algorithme regarde les k plus proches voisins de cette donnée dans l’ensemble d’apprentissage.
L’algorithme des k-plus proches voisins pour la classificatiion et contrôlé par deux paramètres : le nombre de voisin et la distance utilisée pour mesurer le proximité
En pratique un nombre de voisins entre 3 et 5 fonctionne assez bien, on peut toutefois déterminer le meilleur k en testant plusieurs valeurs.
Pour la distance c’est un peu plus complexe c’est pourquoi nous avons laissé la valeur par défaut : la distance euclidienne.
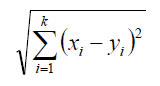
Un inconvénient de l’algorithme k-NN est qu’il doit conserver toutes les données d’entraînement en mémoire. Toutefois il donne d’assez bons résultats pour les jeux de données de petite taille.
Déterminons un k :
#############################################################################
#Méthode des k-NN
nMax=20
myTrainScore = np.zeros(shape=nMax)
myTestScore = np.zeros(shape=nMax)
#myF1Score = np.zeros(shape=nMax) #score F1 abandonné
for n in range(1,nMax) :
knn = KNeighborsClassifier(n_neighbors=n)
knn.fit(X_train, y_train)
myTrainScore[n]=knn.score(X_train,y_train)
print("Training set score: {:.3f}".format(knn.score(X_train,y_train))) #
myTestScore[n]=knn.score(X_test,y_test)
print("Test set score: {:.4f}".format(knn.score(X_test,y_test))) #
#Graphique train score vs test score
sns.set() #paramètres esthétiques ressemble à ggplot par défaut.
fig, ax = plt.subplots() #un seul plot
sns.lineplot(x=np.arange(1,nMax), y=myTrainScore[1:nMax])
sns.lineplot(x=np.arange(1,nMax), y=myTestScore[1:nMax], color='red')
fig.suptitle('On obtient déjà des résultats satisfaisants avec peu de variables.', fontsize=14, fontweight='bold')
ax.set(xlabel='n neighbors', ylabel='Train (bleu) / Test (rouge)',
title="Attention il s'agit ici d'une étude sur un seul site")
fig.text(.3,-.06,"Classification Knn - un seul site - Position dans 2 groupes \n vs variables construites en fonction des n voisins",
fontsize=9)
#plt.show()
fig.savefig("GSC1-KNN-Classifier-2groups.png", bbox_inches="tight", dpi=600)
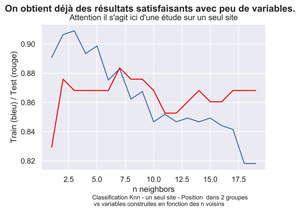
Le meilleur test score (en rouge ) est obtenu avec k=7.
#on choist le le premier n_neighbor ou myF1Score est le plus grand
#à vérifier toutefois en regardant la courbe.
indices = np.where(myF1Score == np.amax(myF1Score))
n_neighbor = indices[0][0]
n_neighbor
knn = KNeighborsClassifier(n_neighbors=n_neighbor)
knn.fit(X_train, y_train)
print("N neighbor="+str(n_neighbor))
print("Training set score: {:.3f}".format(knn.score(X_train,y_train))) #
print("Test set score: {:.4f}".format(knn.score(X_test,y_test))) #
y_pred=knn.predict(X_Scaled)
print("F1-Score : {:.4f}".format(f1_score(y, y_pred, average ='weighted')))
#f1Score retenu pour knn 0.8944
N neighbor=7
Training set score: 0.883
Test set score: 0.8837
Distribution des pages dans les groupes
#par curiosité regardons la distribution des pages dans les groupes
sns.set() #paramètres esthétiques ressemble à ggplot par défaut.
fig, ax = plt.subplots() #un seul plot
sns.countplot(dfGSC1['group'], order=reversed(dfGSC1['group'].value_counts().index))
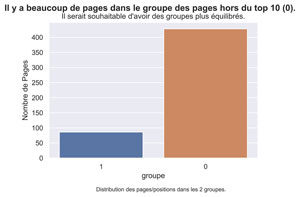
fig.suptitle('Il y a beaucoup de pages dans le groupe des pages hors du top 10 (0).', fontsize=14, fontweight='bold')
ax.set(xlabel='groupe', ylabel='Nombre de Pages',
title="Il serait souhaitable d'avoir des groupes plus équilibrés.")
fig.text(.3,-.06,"Distribution des pages/positions dans les 2 groupes.",
fontsize=9)
#plt.show()
fig.savefig("GSC1-Distribution-2groups.png", bbox_inches="tight", dpi=600)
Modèles Linéaires
Nous allons tester deux modèles linéaires : LogisticRegression et LinearSVC. Pour LogisticRegression on va faire varier le paramètre C qui sert à contrôler l’intensité de la régularisation.
##################################################################################
#Classification linéaire 1 : Régression Logistique
#on faire varier C : inverse of regularization strength; must be a positive float.
#Like in support vector machines, smaller values specify stronger regularization.
logreg = LogisticRegression(solver='lbfgs').fit(X_train,y_train)
print("Training set score: {:.3f}".format(logreg.score(X_train,y_train)))
print("Test set score: {:.3f}".format(logreg.score(X_test,y_test)))
#0.876 pas mieux que knn (knn : 0.8837 )
logreg100 = LogisticRegression(C=100, solver='lbfgs').fit(X_train,y_train)
print("Training set score: {:.3f}".format(logreg100.score(X_train,y_train)))
print("Test set score: {:.3f}".format(logreg100.score(X_test,y_test)))
# 0.884 légèrement mieux que knn (knn : 0.8837 ) <- !!!!!!!!!!!!!
logreg001 = LogisticRegression(C=0.01, solver='lbfgs').fit(X_train,y_train)
print("Training set score: {:.3f}".format(logreg001.score(X_train,y_train)))
print("Test set score: {:.3f}".format(logreg001.score(X_test,y_test)))
# 0.868 moin bien que logreg standard (0,876) et knn (knn : 0.8837 )
#################################################################################
#Classification linéaire 2 : machine à vecteurs supports linéaire (linear SVC).
LinSVC = LinearSVC(max_iter=10000).fit(X_train,y_train)
print("Training set score: {:.3f}".format(LinSVC.score(X_train,y_train)))
print("Test set score: {:.3f}".format(LinSVC.score(X_test,y_test)))
# 0.876 pas mieux que KNN egal à loreg standard
#-> on selectionne logreg100
Importance des variables.
Nous allons visualiser l’importance et le sens des variables peou la régression Logistique avec C=100. Celle qui a donné le meilleur test Score avec 0.884
#######################################################################
# Affichage de l'importance des variables pour logreg100
#######################################################################
signed_feature_importance = logreg100.coef_[0] #pour afficher le sens
feature_importance = abs(logreg100.coef_[0]) #pous classer par importance
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + .5 #pour l'affichage au milieu de la barre
sns.set() #paramètres esthétiques ressemble à ggplot par défaut.
fig, ax = plt.subplots() #un seul plot
ax.barh(pos, signed_feature_importance[sorted_idx], align='center')
ax.set_yticks(pos)
ax.set_yticklabels(np.array(X.columns)[sorted_idx], fontsize=8)
fig.suptitle("La longueur du chemin en caractères influence positivement le modèle \n alors que c'est l'inverse en nombre de mots.\nLes variables propres au site n'influent pas car nous sommes sur 1 seul site.", fontsize=10)
ax.set(xlabel='Importance Relative des variables')
fig.text(.3,-.06,"Régression Logistique C=100 - 1 seul site - Importance des variables",
fontsize=9)
fig.savefig("GSC1-Importance-Variables-C100-2groups.png", bbox_inches="tight", dpi=600)
##########################################################################
# MERCI pour votre attention !
##########################################################################
#on reste dans l'IDE
#if __name__ == '__main__':
# main()
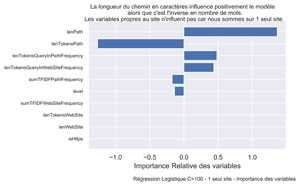
Le fait que lenPath (longueur en caractères) et lenTokensPath (longueur en nombre de mots) sont dans des sens opposés pourrait montrer que le système privilégie les « grands » mots.
Bien que le modèle « interne » puisse fonctionner, nous souhaiterions plutôt nous mesurer à la concurrence dans la suite de nos articles.
Ce modèle interne pourrait toutefois être approfondi pour aider le Web Marketeur à améliorer ses pages sur son site toutes choses égales par ailleurs.
Et vous qu’avez-vous comme résultats ?
A bientôt,
Pierre