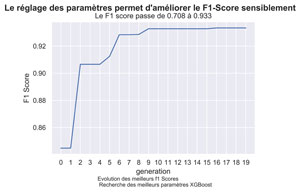
Partager la publication "Optimisation des hyper paramètres XGBoost via un Algorithme Génétique"
Cet article est le dernier d’une série sur le Machine Learning avec Python. Il fait suite à l’article : Classification de pages via le Machine Learning sur un univers de concurrence avec Python – II
Dans cet article précédent, nous avions notamment calculé un modèle XGBoost avec des paramètres standards sur nos données de pages Web afin de prédire leurs positions dans les SERPs de Google.
Ce calcul avait mis en évidence un test -Score de 0,734 encourageant mais que nous pensons pouvoir améliorer en optimisant les paramètres d’XGBoost via un algorithme génétique.
Apprentissage par renforcement
Avant d’aborder les algorithmes génétiques décrivons succinctement ce qu’est l’apprentissage par renforcement.

L’apprentissage par renforcement est généralement décrit au moyen d’une interaction entre un agent et son environnement.
L’agent (par exemple un robot ou un bébé) est la chose qui apprend et l’environnement est composé des conditions dans lesquelles a lieu
l’apprentissage.
L’environnement fournit également de l’information sur la qualité d’une réponse via la fonction de gratification.
Pour l’agent qui apprend cela peut signifier : reproduire l’action qui a fourni la plus grande gratification la dernière fois que l’agent a été dans le même état, ou essayer une action différente dans l’espoir d’améliorer la gratification.
Algorithmes génétiques
Les algorithmes génétiques modélisent le mécanisme de l’évolution, ou de la sélection naturelle présentée par Charles Darwin dans son livre « L’origine des espèces ».

Pour ceux qui douteraient encore de la Théorie de Charles Darwin, Il suffit de faire tourner ces algorithmes pour voir que cela marche 🙂 !!!
En particulier, ils modélisent la reproduction sexuée, dans laquelle les deux parents transmettent de l’information génétique à leurs descendants.
Fonctionnement
Le principe est que nous allons faire évoluer une population dans le temps sur n générations.
1 Dans un premier temps on va sélectionner les individus les plus « aptes » à se reproduire. Dans le cadre du machine learning, l’aptitude est mesurée par une « fonction d’aptitude » (ou de qualité ou de pertinence ou fitness en anglais). Dans notre cas nous allons mesurer le Test Score d’XGBoost avec les paramètres déterminés pour « l’individu ». Les hyper paramètres d’XGBoost, qui peuvent varier, correspondent aux gènes.
2 Ensuite nous allons simuler le brassage génétique qui se passe dans la reproduction sexuée. On parle d’enjambement ou entrecroisement ou en anglais crossover/recombination ou encore de recombinaison génétique : « le phénomène conduisant à l’apparition, dans une cellule ou dans un individu, de gènes ou de caractères héréditaires dans une association différente de celle observée chez les cellules ou individus parentaux » (Wikipédia)
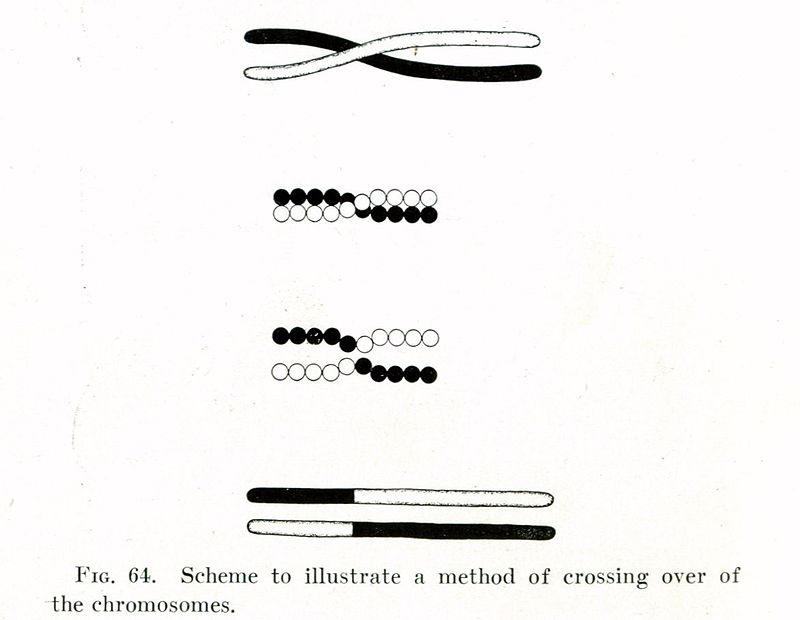
3 Nous allons ensuite simuler les mutations. Dans la nature il s’agit des changements de la séquence d’ADN d’un gène. Dans notre cas, il s’agit d’un changement de la valeur d’un hyper paramètre d’XGBoost tiré au hasard.
Nous allons ensuite un peu ‘forcer » la nature :
4 A la manière d’un éleveur nous allons pratiquer « l’Elitisme« . C’est à dire que nous allons conserver des individus exceptionnels à la génération suivante, un peu comme on garde un reproducteur ou un étalon.
5 Nous allons aussi procéder à des « tournois« , c’est à dire que nous allons comparer les populations de parents et d’enfants et nous allons conserver les meilleurs. Comme un éleveur qui garderait les meilleurs individus dans son troupeau quelles que soient leurs générations et vendrait les autres.
De quoi aurons nous besoin ?
Nous travaillons avec la version Python Anaconda qui comprend les bibliothèques nécessaires au traitement de données et au Machine Learning.
Pour le jeu de données nous partons du fichier dfQPPS7.csv, que vous pouvez retrouver sur notre Github : https://github.com/Anakeyn/XGBoostParametersTuningGeneticAlgorithm/raw/master/dfQPPS7.csv
Code Source
Vous pouvez soit copier/coller les morceaux de codes ci-dessous, soit récupérer gratuitement les codes sources en entier dans notre boutique à l’adresse : https://www.anakeyn.com/boutique/produit/script-python-optimisation-xgboost-avec-algorithme-genetique/
Algorithme génétique
Dans un premier temps nous allons décrire l’algorithme génétique qui est dans un programme Python à part « ga_XGBClassifier.py« .
Ce programme s’inspire :
- Du code réalisé par Stephen Marsland et présenté au chapitre 10 de son livre » Machine Learning: An Algorithmic Perspective (2nd Edition) ». Ce code présente une classe pour un algorithme génétique « généraliste ». Le code original est aussi disponible sur Github à l’adresse https://github.com/alexsosn/MarslandMLAlgo/blob/master/Ch10/ga.py
- Du code de Mohit Jain qui traite plus spécifiquement du même thème que cet article, à savoir l’optimisation des paramètres XGBoost. Le code est disponible sur son Github à l’adresse https://github.com/mjain72/Hyperparameter-tuning-in-XGBoost-using-genetic-algorithm
Rappelons que dans notre article précédent Classification de pages via le Machine Learning sur un univers de concurrence avec Python – II nous étions arrivé à un test Score de 0.734 qui était meilleurs qu’avec les modèles linaires calculés. Les paramètres de base étaient les suivants :
{‘base_score’: 0.5, ‘booster’: ‘gbtree’, ‘colsample_bylevel’: 1, ‘colsample_bytree’: 1, ‘gamma’: 0, ‘learning_rate’: 0.1, ‘max_delta_step’: 0, ‘max_depth’: 3, ‘min_child_weight’: 1, ‘missing’: None, ‘n_estimators’: 100, ‘nthread’: 1, ‘objective’: ‘binary:logistic’, ‘reg_alpha’: 0, ‘reg_lambda’: 1, ‘scale_pos_weight’: 1, ‘seed’: 0, ‘silent’: True, ‘subsample’: 1, ‘verbosity’: 0}
Les 7 paramètres en gras sont ceux que nous ferons varier par la suite.
Les chromosomes comportent 7 gènes qui correspondent ici aux paramètres à affiner. Contrairement à l’algorithme de Stephen Marsland dont les gènes n’ont que 2 valeurs possibles (0 ou 1), les gènes ici ont des codifications différentes les uns des autres et qui correspondent aux valeurs que peuvent potentiellement prendre les hyper paramètres.
Ainsi nous avons les gènes suivants :
- learningRate : peut varier de 0.01 à 1
- nEstimators : peut varier de 10 à 2000, par
pas de 25 - maxDepth : peut varier de 1 à 15
- minChildWeight : peut varier de 0.01 à 10.0
- gammaValue : peut varier de 0.01 à 10
- subSample : peut varier de 0.01 à 1.0
- colSampleByTree : 0.01 à 1.0
Notez bien aussi les paramètres en entrée de la classe ga_XGBClassifier :
- fitnessFunction : nom de la fonction d’aptitude, il s’agit du calcul du test Score pour XGBoost, celle ci sera décrite plus loin dans la partie « implémentation ».
- nEpochs : nombre de générations
- X : données des variables explicatives pour XGBoost
- y : données de la variable à expliquer pour XGBoost
- X_train : données des variables explicatives d’entraienement
- X_test : données des variables explicatives de test
- y_train : données de la variable à expliquer d’entrainement
- y_test : données de la variable à expliquer de test
- populationSize : taille la population. 100 par défaut
- crossover : méthode d’enjambement soit à partir d’un point, soit uniforme : i.e. à la moitié.
- nElite : nombre d’individus à conserver lors de la phase d’élitisme. Par défaut : 4
- tournamentOK : est-ce que l’on fait un tournoi ou non. Oui par défaut.
Initialisation de la CLASSE ga_XGBClassifier
les valeurs des paramètres sont tirés au hasard pour chacun des individus de la population de départ.
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Tue Jul 02 22:33:49 2019
@author: Pierre
"""
# Code from Chapter 10 p211 of Machine Learning: An Algorithmic Perspective (2nd Edition)
# by Stephen Marsland (http://stephenmonika.net)
# You are free to use, change, or redistribute the code in any way you wish for
# non-commercial purposes, but please maintain the name of the original author.
# This code comes with no warranty of any kind.
# Stephen Marsland, 2008, 2014
# The Genetic algorithm
# Comment and uncomment fitness functions as appropriate (as an import and the fitnessFunction variable)
# voir original sur Github:
# https://github.com/alexsosn/MarslandMLAlgo/blob/master/Ch10/ga.py
# Modifications par Pierre Rouarch :
# de ga Standard à un ga pour trouver les paramètres de réglages de XGBClassifier
# Inspiré par Mohit Jain - "Hyperparameter tuning in XGBoost using genetic algorithm"
# https://github.com/mjain72/Hyperparameter-tuning-in-XGBoost-using-genetic-algorithm
#on a aussi enlevé le plot qui peut être fait à l'extérieur de la classe.
import numpy as np
import random
class ga_XGBClassifier:
def __init__(self,fitnessFunction,nEpochs, X, y, X_train, X_test, y_train, y_test, populationSize=100,crossover='un',nElite=4,tournamentOK=True):
""" Constructor"""
self.stringLength = 7 #ici on a 7 paramètres donc 7 gènes
# Population size should be even
if np.mod(populationSize,2)==0:
self.populationSize = populationSize
else:
self.populationSize = populationSize+1
#MutationProb non utilisé en fait la mutation est de 1/7 car on mute un seul paramètres à la fois
self.nEpochs = nEpochs #nombre de générations
self.bestfit = np.zeros(self.nEpochs) #raz de bestfit
self.bestParams = np.zeros((self.nEpochs,7)) #raz de bestParams
self.fitness = np.zeros(self.populationSize) #pour conserver les derniers fitness #pas sur que cela soit utile
self.fitnessFunction = fitnessFunction #ici calcul du Test Score de XGBoostClassifier
self.crossover = crossover #type de crossover 'un' uniforme ou 'sp'
self.nElite = nElite #nombre de parents conservés dans l'élitisme
self.tournamentOK = tournamentOK #Est-ce que l'on fait le tournoi ?
####### Données pour XGBClassifier
self.X = X
self.y = y
self.X_train = X_train
self.X_test = X_test
self.y_train = y_train
self.y_test = y_test
#### Construction de la population #######
self.learningRate = np.empty([self.populationSize, 1])
self.nEstimators = np.empty([self.populationSize, 1], dtype = np.uint8)
self.maxDepth = np.empty([self.populationSize, 1], dtype = np.uint8)
self.minChildWeight = np.empty([self.populationSize, 1])
self.gammaValue = np.empty([self.populationSize, 1])
self.subSample = np.empty([self.populationSize, 1])
self.colSampleByTree = np.empty([self.populationSize, 1])
#valeurs de départ au hasard.
for i in range(self.populationSize):
#print(i)
self.learningRate[i] = round(random.uniform(0.01, 1), 2)
self.nEstimators[i] = int(random.randrange(10, 2000, step = 25))
self.maxDepth[i] = int(random.randrange(1, 15, step= 1))
self.minChildWeight[i] = round(random.uniform(0.01, 10.0), 2)
self.gammaValue[i] = round(random.uniform(0.01, 10.0), 2)
self.subSample[i] = round(random.uniform(0.01, 1.0), 2)
self.colSampleByTree[i] = round(random.uniform(0.01, 1.0), 2)
self.population = np.concatenate((self.learningRate, self.nEstimators, self.maxDepth, self.minChildWeight, self.gammaValue, self.subSample, self.colSampleByTree), axis= 1)
Boucle dans les generations
#boucle
def runGA(self):
"""The basic loop"""
#commenter les print si vous trouvez qu'il y a trop d'affichage
print("ca tourne")
self.bestfit = np.zeros(self.nEpochs) #raz de bestfit
self.bestParams = np.zeros((self.nEpochs,7)) #raz de bestParams
for i in range(self.nEpochs):
print("boucle génération = "+str(i))
# Compute fitness of the population
fitness = (self.fitnessFunction)(self.population, self.X, self.y, self.X_train, self.X_test, self.y_train, self.y_test )
print ("Liste des fitness pour cette génération ", i, fitness)
if (np.mod(i,1)==0):
print("Meilleurs paramètres de cette génération ", i, self.population[np.argmax(fitness),:])
print("Meilleur Fitness de cette génération ", i, max(fitness)) #il affiche le meilleur toutes les x iterations
#sauvegarde dans l'objet pour utilisation extérieure.(notamment plotting)
self.bestParams[i] = self.population[np.argmax(fitness),:] #meilleurs paramètres de cette génération
self.bestfit[i] = max(fitness) #on conserve le meilleur fitness de la génération i pour faire un graphique
self.fitness = fitness #on conserve les derniers fitness de cette génération #pas vraiment utile
#Pick parents -- can do in order since they are randomised
#récupere les parents les plus aptes
newPopulation = self.fps(self.population,fitness) #prend les individus les plus aptes en priorité.
# Apply the genetic operators
if self.crossover == 'sp': #croisement à partir d'un point
newPopulation = self.spCrossover(newPopulation)
elif self.crossover == 'un': #croisement uniforme
newPopulation = self.uniformCrossover(newPopulation)
#Mutation
newPopulation = self.mutation(newPopulation) #mutation sur un des paramètres au hasard
# Apply elitism
if self.nElite>0:
newPopulation = self.elitism(self.population,newPopulation,fitness)
#apply tournoi
if self.tournamentOK :
newPopulation = self.tournament(self.population,newPopulation,fitness,self.fitnessFunction, self.X, self.y, self.X_train, self.X_test, self.y_train, self.y_test)
self.population = newPopulation #nouvelle population pour le tour suivant
Sélection des Parents
#sélection des parents
def fps(self,population,fitness): #echantillonage pour reproduction.
print("Recupération des parents")
print("fitness en entrée", fitness)
# Scale fitness by total fitness
fitness = fitness/np.sum(fitness)
fitness = 10*fitness/fitness.max()
print("fitness transformé", fitness)
# Put repeated copies of each string in according to fitness
# Deal with strings with very low fitness
j=0
while np.round(fitness[j])<1:
j = j+1
print("Produit de Kronecker ", j, "fitness ", fitness[j])
#Produit de Kronecker : echantillonage au hasard à probabilité inégale (parce que aptitude)
#simule la sélection naturelle. Plus le chromosome est apte plus il a de chance d'être sélectionné.
newPopulation = np.kron(np.ones((int(np.round(fitness[j])),1)),population[j,:])
# Add multiple copies of strings into the newPopulation #ici les suivants.
for i in range(j+1,self.populationSize):
print("Add multiple copies i = ", i)
if np.round(fitness[i])>=1:
print("Avec fitness : ", fitness[i])
newPopulation = np.concatenate((newPopulation,np.kron(np.ones((int(np.round(fitness[i])),1)),population[i,:])),axis=0)
# Shuffle the order (note that there are still too many) on prend les n premiers : populationSize
indices = list(range(np.shape(newPopulation)[0]))
np.random.shuffle(indices)
newPopulation = newPopulation[indices[:self.populationSize],:]
return newPopulation
Enjambement ou CROSSOVER (Brassage génétique)
#croisement à partir d'un point
def spCrossover(self,population):
print("Single point crossover")
# Single point crossover
newPopulation = np.zeros(np.shape(population))
crossoverPoint = np.random.randint(0,self.stringLength,self.populationSize)
for i in range(0,self.populationSize,2):
newPopulation[i,:crossoverPoint[i]] = population[i,:crossoverPoint[i]]
newPopulation[i+1,:crossoverPoint[i]] = population[i+1,:crossoverPoint[i]]
newPopulation[i,crossoverPoint[i]:] = population[i+1,crossoverPoint[i]:]
newPopulation[i+1,crossoverPoint[i]:] = population[i,crossoverPoint[i]:]
return newPopulation
#croisement uniforme
def uniformCrossover(self,population):
print("Uniform crossover")
# Uniform crossover
newPopulation = np.zeros(np.shape(population))
which = np.random.rand(self.populationSize,self.stringLength)
which1 = which>=0.5
for i in range(0,self.populationSize,2):
newPopulation[i,:] = population[i,:]*which1[i,:] + population[i+1,:]*(1-which1[i,:])
newPopulation[i+1,:] = population[i,:]*(1-which1[i,:]) + population[i+1,:]*which1[i,:]
return newPopulation
Mutation
Un seul paramètre est muté au hasard.
#mutation
def mutation(self,population):
#Attention ici la mutation se fait sur un seul paramètre/gène à la fois.
#Define minimum and maximum values allowed for each parameter
minMaxValue = np.zeros((7, 2)) #pour enregistrer les valeurs. Min et Max
minMaxValue[0:] = [0.01, 1.0] #min/max learning rate
minMaxValue[1, :] = [10, 2000] #min/max n_estimators
minMaxValue[2, :] = [1, 15] #min/max depth
minMaxValue[3, :] = [0, 10] #min/max child_weight
minMaxValue[4, :] = [0.01, 10.0] #min/max gamma
minMaxValue[5, :] = [0.01, 1.0] #min/maxsubsample
minMaxValue[6, :] = [0.01, 1.0] #min/maxcolsample_bytree
# Mutation changes a single gene in each offspring randomly.
mutationValue = 0
parameterSelect = np.random.randint(0, 7, 1) #parametre au hasard
print("Mutation Paramètre sélectionné : "+str(parameterSelect))
if parameterSelect == 0: #learning_rate
mutationValue = round(np.random.uniform(-0.5, 0.5), 2)
if parameterSelect == 1: #n_estimators
mutationValue = np.random.randint(-200, 200, 1)
if parameterSelect == 2: #max_depth
mutationValue = np.random.randint(-5, 5, 1)
if parameterSelect == 3: #min_child_weight
mutationValue = round(np.random.uniform(-5, 5), 2)
if parameterSelect == 4: #gamma
mutationValue = round(np.random.uniform(-2, 2), 2)
if parameterSelect == 5: #subsample
mutationValue = round(np.random.uniform(-0.5, 0.5), 2)
if parameterSelect == 6: #colsample
mutationValue = round(np.random.uniform(-0.5, 0.5), 2)
#introduce mutation by changing one parameter, and set to max or min if it goes out of range
for idx in range(population.shape[0]):
population[idx, parameterSelect] = population[idx, parameterSelect] + mutationValue
if(population[idx, parameterSelect] > minMaxValue[parameterSelect, 1]):
population[idx, parameterSelect] = minMaxValue[parameterSelect, 1]
if(population[idx, parameterSelect] < minMaxValue[parameterSelect, 0]):
population[idx, parameterSelect] = minMaxValue[parameterSelect, 0]
return population
Elistisme
#on choisit les nElite meilleurs - 4 par défaut
def elitism(self,oldPopulation,population,fitness):
print("Elitisme")
best = np.argsort(fitness)
best = np.squeeze(oldPopulation[best[-self.nElite:],:])
indices = list(range(np.shape(population)[0]))
np.random.shuffle(indices)
population = population[indices,:]
population[0:self.nElite,:] = best
return population
Tournois
#les 2 meilleurs parmi les parents et leurs enfants.
def tournament(self,oldPopulation,population,fitness,fitnessFunction, X, y, X_train, X_test, y_train, y_test):
print("Début de Tournoi")
newFitness = (self.fitnessFunction)(population, X, y, X_train, X_test, y_train, y_test)
print("Nouveau Fitness", newFitness)
print("on va tourner ", np.shape(population)[0], " fois par pas de 2" )
for i in range(0,np.shape(population)[0],2):
f = np.concatenate((fitness[i:i+2],newFitness[i:i+2]),axis=0)
indices = np.argsort(f)
if indices[-1]<2 and indices[-2]<2:
population[i,:] = oldPopulation[i,:]
population[i+1,:] = oldPopulation[i+1,:]
elif indices[-1]<2:
if indices[0]>=2:
population[i+indices[0]-2,:] = oldPopulation[i+indices[-1]]
else:
population[i+indices[1]-2,:] = oldPopulation[i+indices[-1]]
elif indices[-2]<2:
if indices[0]>=2:
population[i+indices[0]-2,:] = oldPopulation[i+indices[-2]]
else:
population[i+indices[1]-2,:] = oldPopulation[i+indices[-2]]
print("Fin de Tournoi")
return population
Implémentation / test
Afin de tester cet algorithme génétique nous allons revenir au point ou nous en étions précédemment avec notre XGBoost concernant la classification des pages Web.
Vous pouvez bien sûr avoir une autre problématique à résoudre pour tester ga_XGBClassifier.py. Veillez toutefois à avoir une fonction d’aptitude pertinente.
Cette partie est conservée dans le programme XGBoostParametersTuningGeneticAlgorithm.py que vous pouvez retrouver sur notre Github.
Chargement des Bibliothèques UTILES
# -*- coding: utf-8 -*- """ Created on Tue Jul 02 18:39:18 2019 @author: Pierre """ ########################################################################## # XGBoostParametersTuningGeneticAlgorithm - modifié le 26/11/2011 # Auteur : Pierre Rouarch - Licence GPL 3 # Exemple d'utilisation d'un algorithme génétique pour améliorer les performances # D'un algorithme XGBoost # la fonction de fitness ou d'évaluation se base sur le test score ##################################################################################### ################################################################### # On démarre ici ################################################################### #Chargement des bibliothèques générales utiles import numpy as np #pour les vecteurs et tableaux notamment import matplotlib.pyplot as plt #pour les graphiques import pandas as pd #pour les Dataframes ou tableaux de données import seaborn as sns #graphiques étendues import os from xgboost import XGBClassifier from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler #pour les scores #from sklearn.metrics import f1_score #from sklearn.metrics import matthews_corrcoef print(os.getcwd()) #verif #mon répertoire sur ma machine - nécessaire quand on fait tourner le programme #par morceaux dans Spyder. #myPath = "C:/Users/Pierre/MyPath" #os.chdir(myPath) #modification du path #print(os.getcwd()) #verif
Récupération des DONNéES ET PRéPARATION
#############################################################
# On revient au Machine Learning
#####################################################################
#Lecture des données suite à scraping ############
dfQPPS8 = pd.read_csv("dfQPPS7.csv")
dfQPPS8.info(verbose=True) # 12194 enregistrements.
dfQPPS8.reset_index(inplace=True, drop=True)
#Variables explicatives
X = dfQPPS8[['isHttps', 'level',
'lenWebSite', 'lenTokensWebSite', 'lenTokensQueryInWebSiteFrequency', 'sumTFIDFWebSiteFrequency',
'lenPath', 'lenTokensPath', 'lenTokensQueryInPathFrequency' , 'sumTFIDFPathFrequency',
'lenTitle', 'lenTokensTitle', 'lenTokensQueryInTitleFrequency', 'sumTFIDFTitleFrequency',
'lenDescription', 'lenTokensDescription', 'lenTokensQueryInDescriptionFrequency', 'sumTFIDFDescriptionFrequency',
'lenH1', 'lenTokensH1', 'lenTokensQueryInH1Frequency' , 'sumTFIDFH1Frequency',
'lenH2', 'lenTokensH2', 'lenTokensQueryInH2Frequency' , 'sumTFIDFH2Frequency',
'lenH3', 'lenTokensH3', 'lenTokensQueryInH3Frequency' , 'sumTFIDFH3Frequency',
'lenH4', 'lenTokensH4','lenTokensQueryInH4Frequency', 'sumTFIDFH4Frequency',
'lenH5', 'lenTokensH5', 'lenTokensQueryInH5Frequency', 'sumTFIDFH5Frequency',
'lenH6', 'lenTokensH6', 'lenTokensQueryInH6Frequency', 'sumTFIDFH6Frequency',
'lenB', 'lenTokensB', 'lenTokensQueryInBFrequency', 'sumTFIDFBFrequency',
'lenEM', 'lenTokensEM', 'lenTokensQueryInEMFrequency', 'sumTFIDFEMFrequency',
'lenStrong', 'lenTokensStrong', 'lenTokensQueryInStrongFrequency', 'sumTFIDFStrongFrequency',
'lenBody', 'lenTokensBody', 'lenTokensQueryInBodyFrequency', 'sumTFIDFBodyFrequency',
'elapsedTime', 'nbrInternalLinks', 'nbrExternalLinks' ]] #variables explicatives
X.info()
y = dfQPPS8['group']
#on va scaler
scaler = StandardScaler()
scaler.fit(X)
X_Scaled = pd.DataFrame(scaler.transform(X.values), columns=X.columns, index=X.index)
X_Scaled.info()
#on choisit random_state = 42 en hommage à La grande question sur la vie, l'univers et le reste
#dans "Le Guide du voyageur galactique" par Douglas Adams. Ceci afin d'avoir le même split
#tout au long de notre étude.
X_train, X_test, y_train, y_test = train_test_split(X_Scaled,y, random_state=42)
XGBoost avec les paramètres par défaut
#########################################################################
# XGBOOST
##########################################################################
#xgboost avec parametres standards par défaut
myXGBoost = XGBClassifier().fit(X_train,y_train)
print("Training set score: {:.3f}".format(myXGBoost.score(X_train,y_train)))
print("Test set score: {:.3f}".format(myXGBoost.score(X_test,y_test)))
baseTestScore = myXGBoost.score(X_test,y_test)
#parametres par défaut
myXGBoost.get_xgb_params()
Fonction d’APTITUDE ou de FITNESS
Cette fonction renvoie les Test Scores pour une population.
########################### Fonction de Fitness utilisée ici
#La fonction d'évaluation est basée sur le test score
#on calcule le F1 score pour chaque XGBClassifier
def train_populationClassifier(population, X, y, X_train, X_test, y_train, y_test):
print("Fitness Function")
TestScore = []
for i in range(population.shape[0]):
print("Fitness Boucle dans la population "+str(i))
param = { 'objective':'binary:logistic',
'learning_rate': population[i][0],
'n_estimators': int(population[i][1]),
'max_depth': int(population[i][2]),
'min_child_weight': population[i][3],
'gamma': population[i][4],
'subsample': population[i][5],
'colsample_bytree': population[i][6],
'seed': 24}
myXGBClassifier = XGBClassifier(**param).fit(X_train,y_train)
#preds=myXGBClassifier.predict(X_Scaled)
#preds = preds>0.5
TestScore.append(round(myXGBClassifier.score(X_test,y_test), 4))
return TestScore
###### / fonction de Fitness
UtilisatioN de GA_XGBClassifier
Ici on prendra 20 générations de 10 individus.
######################################################################
#on utilise ga_XGBClassifier - Attention cela dure un moment !!!!
###################################################################"
iterations=20 #nombre de générations
import ga_XGBClassifier #import de la classe
#on instancie un objet de classe ga_XGBClassifier
myGA = ga_XGBClassifier.ga_XGBClassifier(train_populationClassifier,
nEpochs=iterations, X=X_Scaled, y=y,
X_train=X_train, X_test=X_test,
y_train=y_train, y_test=y_test,
populationSize=10,
crossover='un',nElite=4,tournamentOK=True)
myGA.runGA() #on boucle dans l'objet créé
myGA.bestParams #meileurs parametres par génération
myGA.bestfit #meileur fitness par génération
nMax=myGA.bestfit.size
GRAPHIQUE DE L’EVOLUTION DES MEILLEURS F1 SCORES
###########################################################
#Graphique Evolution des meilleurs test Scores
sns.set() #paramètres esthétiques ressemble à ggplot par défaut.
fig, ax = plt.subplots() #un seul plot
sns.lineplot(x=np.arange(0,nMax), y=myGA.bestfit[0:nMax])
fig.suptitle("Le réglage des paramètres permet d'améliorer le test Score sensiblement", fontsize=14, fontweight='bold')
ax.set(xlabel='generation', ylabel='test Score',
title="Le Test score passe de "+"{0:.3f}".format(baseTestScore)+" à "+"{0:.3f}".format(myGA.bestfit[nMax-1]) )
ax.xaxis.set_ticks(range(nMax))
fig.text(.3,-.06,"Evolution des meilleurs Test Scores \n Recherche des meilleurs paramètres XGBoost",
fontsize=9)
#plt.show()
fig.savefig("QPPS6-GA-XGBClassifier-BestTestScores.png", bbox_inches="tight", dpi=600)
##########################################################################
# MERCI pour votre attention !
##########################################################################
#on reste dans l'IDE
#if __name__ == '__main__':
# main()
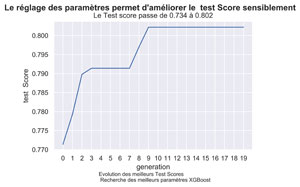
Comme on le voit, le Test Score c’est amélioré sensiblement de pour arriver à 0.8022 . Il est même meilleur que celui que l’on avait eu précédemment pour KNN à savoir 0.7553.
XGBoost, s’il est bien paramétré peut être un bon candidat pour classer les pages Web.
Et vous ? qu’avez vous obtenu avec vos données ?
A Bientôt,
Pierre