Partager la publication "Détection du trafic Web significatif avec Python"
Précédemment, nous avions vu comment détecter les jours de trafic significatif sur son site Web avec R.
Pour ne pas faire de jaloux nous allons maintenant déterminer cela avec Python.
De quoi aurons-nous besoin ?
Python Anaconda
Comme précédemment, nous vous invitons à utiliser la version de Python Anaconda qui contient toutes les bibliothèques statistiques nécessaires et les outils suivants :
- Anaconda Navigator qui permet d’accéder à de nombreux autres outils.
- L’invite de commande Anaconda Prompt qui permet notamment d’utiliser le gestionnaire de paquets « Conda » afin d’ajouter des bibliothèques à votre environnement Python.
- Spyder : l’environnement de développement intégré fourni par défaut.
Anaconda est compatible Windows, Mac et Linux. Rendez vous sur la page de téléchargement d’Anaconda Distribution pour télécharger la version qui vous convient.
Test Tau de Thompson modifié
Nous n’avons pas trouvé de bibliothèque équivalente à AnomalyDetection de R en Python. Si vous en connaissez…
C’est pourquoi nous allons calculer à la main ces anomalies en utilisant la méthode du Test Tau de Thompson modifié. Ce test est présenté sur la page « Donnée aberrante » de Wikipedia.
Nous reviendrons en détail sur cette méthode plus bas.
Jeu de données
Comme avec R, et afin d’illustrer notre propos, nous partirons du jeu de données de l’association Networking Morbihan que nous avons déjà utilisé précédemment.
Ce jeu de données a été récupéré via l’API Google Analytics dont on a ensuite nettoyé le Spam : voir ici pour cette opération en Python.
Vous pouvez télécharger ce jeu de données ainsi que le code source en entier gratuitement dans notre boutique à l’adresse : https://www.anakeyn.com/boutique/produit/script-python-detection-trafic-web-significatif/ . Dézippez tous les fichiers et sauvegardez-les dans le même répertoire.
Code source
Vous pouvez copier/coller les bouts de code dans les zones de code ou sinon tout télécharger depuis notre boutique : https://www.anakeyn.com/boutique/produit/script-python-detection-trafic-web-significatif/
Récupération des données :
Les données sont récupérées à partir du fichier dfPageViews.csv et mises en forme pour avoir un enregistrement par jour.
# -*- coding: utf-8 -*-
"""
Created on Tue May 23 10:50:38 2019
@author: Pierre
"""
#########################################################################
# DetectSignificatnWebTrafficPython
# Détection de trafic Web significatif avec Python
# Auteur : Pierre Rouarch 2019
# Données : Issues de l'API de Google Analytics -
# Comme illustration Nous allons travailler sur les données du site
# https://www.networking-morbihan.com
# Site de l'association Networking Morbihan :
# https://github.com/Anakeyn/DetectSignificantWebTrafficPython/raw/master/dfPageViews.zip
#.
#############################################################
# On démarre ici !!!!
#############################################################
#def main(): #on ne va pas utiliser le main car on reste dans Spyder
#Chargement des bibliothèques utiles
import numpy as np #pour les vecteurs et tableaux notamment
import matplotlib.pyplot as plt #pour les graphiques
import scipy as sp #pour l'analyse statistique
import pandas as pd #pour les Dataframes ou tableaux de données
import seaborn as sns #graphiques étendues
import math #notamment pour sqrt()
from datetime import timedelta
from scipy import stats
#pip install scikit-misc #pas d'install conda ???
from skmisc import loess #pour methode Loess compatible avec stat_smooth
#conda install -c conda-forge plotnine
from plotnine import * #pour ggplot like
#conda install -c conda-forge mizani
from mizani.breaks import date_breaks #pour personnaliser les dates affichées
#Changement du répertoire par défaut pour mettre les fichiers de sauvegarde
#dans le même répertoire que le script.
import os
print(os.getcwd()) #verif
#mon répertoire sur ma machine - nécessaire quand on fait tourner le programme
#par morceaux dans Spyder.
#myPath = "C:/Users/Pierre/CHEMIN"
#os.chdir(myPath) #modification du path
#print(os.getcwd()) #verif
###############################################################################
#Récupération du fichiers de données
###############################################################################
myDateToParse = ['date'] #pour parser la variable date en datetime sinon object
dfPageViews = pd.read_csv("dfPageViews.csv", sep=";", dtype={'Année':object}, parse_dates=myDateToParse)
#verifs
dfPageViews.dtypes
dfPageViews.count() #72821 enregistrements
dfPageViews.head(20)
##############################################################################
#creation de la dataframe daily_data par jour
dfDatePV = dfPageViews[['date', 'pageviews']].copy() #nouveau dataframe avec que la date et le nombre de pages vues
daily_data = dfDatePV.groupby(dfDatePV['date']).count() #
#dans l'opération précédente la date est partie dans l'index
daily_data['date'] = daily_data.index #recrée la colonne date.
daily_data['cnt_ma30'] = daily_data['pageviews'].rolling(window=30).mean()
daily_data['Année'] = daily_data['date'].astype(str).str[:4]
daily_data['DayOfYear'] = daily_data['date'].dt.dayofyear #récupère la date du jour
daily_data.reset_index(inplace=True, drop=True) #on reindexe
#Graphique Moyenne Mobile 30 jours.
sns.set() #paramètres esthétiques ressemble à ggplot par défaut.
fig, ax = plt.subplots() #un seul plot
sns.lineplot(x='DayOfYear', y='cnt_ma30', hue='Année', data= daily_data,
palette=sns.color_palette("husl",n_colors=8))
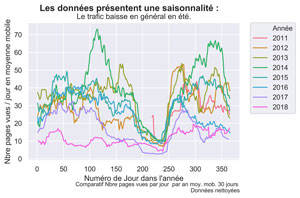
fig.suptitle("Les données présentent une saisonnalité : ", fontsize=14, fontweight='bold')
ax.set(xlabel="Numéro de Jour dans l'année", ylabel='Nbre pages vues / jour en moyenne mobile',
title="Le trafic baisse en général en été.")
fig.text(.9,-.05,"Comparatif Nbre pages vues par jour par an moy. mob. 30 jours \n Données nettoyées",
fontsize=9, ha="right")
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
#plt.show()
fig.savefig("PV-Comparatif-mm30.png", bbox_inches="tight", dpi=600)
# Sauvegarde de DailyData en csv pourra servir dans d'autres articles.
daily_data.to_csv("DailyDataCleanPython.csv", sep=";", index=False) #séparateur ;
Utilisation du test Tau de Thompson modifié
Le test Tau de Thompson modifié est une méthode utilisée pour déterminer s’il existe des données aberrantes dans une série de valeurs.
Cette méthode prend en compte l’écart-type et la moyenne de la série et fournit un seuil de rejet déterminée statistiquement.
Déroulement du test :
Etape 1 : On détermine un seuil de rejet en utilisant la formule suivante :
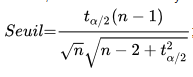
où :

ou tau est la valeur critique provenant de la table de la Loi de Student et n est la taille de l’échantillon.
Remarque : ici pour un intervalle bilatéral à 95 %, on prendra le quantile à 97,5 % dans la table de Student. Pour un échantillon très grand, pour nous n=2658, tau = 1,96.
########################################################################## # Détections des événements significatifs - Données aberrantes # on va utiliser la méthode du Test de Tau de Thompson Modifié # Voir ici https://fr.wikipedia.org/wiki/Donn%C3%A9e_aberrante ########################################################################## #Etape 1 Calcul du Seuil n=daily_data.shape[0] #taille de l'échantilon 2658 #Récupérons la valeur de Tau sur la table de Student tau=1.96 #calculons le seuil de base threshold = (tau*(n-1))/( math.sqrt(n) * math.sqrt(n-2+(math.pow(tau,2))) ) #threshold=1.9585842166773806
Le seuil trouvé est égal à 1.9585842166773806
Etape 2 : On calcule ensuite le z-score de chaque valeur. le z-score est l’écart de la valeur à la moyenne divisé par l’écart-type. Le z-score est comparé ensuite au seuil :
- Si le z-score > seuil, la valeur est une donnée aberrante.
- Si le z-score <= seuil, la valeur n’est pas une donnée aberrante.
#Etape 2 Evaluation du zcore par rapport au seuil # ici z_score = (daily_data['pageviews'] - mean)/std donné # par zcore de scipy.stats mais que l'on aurait pu calculer. à la main from scipy.stats import zscore daily_data['pageviews_zscore'] = zscore(daily_data['pageviews']) myOutliersBase = daily_data[daily_data['pageviews_zscore'] > threshold] len(myOutliersBase) #136 valeurs aberrantes
Le calcul donne 136 valeurs aberrantes. On pourrait utiliser cette valeur, toutefois, pour être cohérent avec R et avoir un nombre de valeurs aberrantes équivalent, nous allons prendre un seuil plus restrictif :
#Finalement on va augmenter le seuil de façon empirique pour réduire le #nombre de valeurs aberrantes à un même niveau de ce que l'on avait avec R threshold = 2.29 myOutliers = daily_data[daily_data['pageviews_zscore'] > threshold] len(myOutliers) #97 valeurs
Pour un seuil à 2,29 on obtient 97 valeurs aberrantes.
Affichage des anomalies sur la courbe des pages vues.
#Graphique Pages vues
sns.set() #paramètres esthétiques ressemble à ggplot par défaut.
fig, ax = plt.subplots() #un seul plot
sns.lineplot(x='date', y='pageviews', data= daily_data)
sns.scatterplot(x='date', y='pageviews', data= myOutliers, color='red')
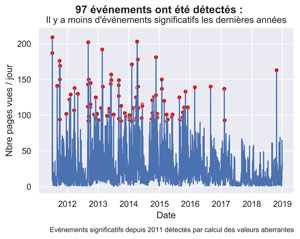
fig.suptitle( str(len(myOutliers)) + " événements ont été détectés : ", fontsize=14, fontweight='bold')
ax.set(xlabel="Date", ylabel='Nbre pages vues / jour',
title="Il y a moins d'événements significatifs les dernières années")
fig.text(.9,-.05,"Evénements significatifs depuis 2011 détectés par calcul des valeurs aberrantes",
fontsize=9, ha="right")
#plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
#plt.show()
fig.savefig("Anoms-Pageviews-s2011.png", bbox_inches="tight", dpi=600)
Affichage des anomalies en moyenne mobile sur 30 jours.
#Affichage sur la courbe des moyennes mobiles sur 30 jours
sns.set() #paramètres esthétiques ressemble à ggplot par défaut.
fig, ax = plt.subplots() #un seul plot
sns.lineplot(x='date', y='cnt_ma30', data= daily_data)
sns.scatterplot(x='date', y='cnt_ma30', data= myOutliers, color='red')
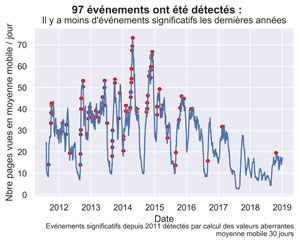
fig.suptitle( str(len(myOutliers)) + " événements ont été détectés : ", fontsize=14, fontweight='bold')
ax.set(xlabel="Date", ylabel='Nbre pages vues en moyenne mobile / jour',
title="Il y a moins d'événements significatifs les dernières années")
fig.text(.9,-.05,"Evénements significatifs depuis 2011 détectés par calcul des valeurs aberrantes\n moyenne mobile 30 jours",
fontsize=9, ha="right")
#plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
#plt.show()
fig.savefig("Anoms-Pageviews-s2011-mm30.png", bbox_inches="tight", dpi=600)
##########################################################################
# MERCI pour votre attention !
##########################################################################
#on reste dans l'IDE
#if __name__ == '__main__':
# main()
Merci pour votre attention.
Dans un prochain article nous verrons si les actions marketing que nous avons menées sont en rapport avec ces augmentations de trafic.
A Bientôt,
Pierre